Desde finales del siglo xix hasta bien pasada la mitad del siglo xx, casi cualquier profesional vinculado a la gráfica hubiese podido listar sin ningún esfuerzo las letras más usadas: etaoin shrdlu. Las máquinas de linotipo presentaban las teclas agrupadas en columnas de a seis, ordenadas de arriba a abajo y de izquierda a derecha según su frecuencia de uso, y cada vez que el operario cometía un error, indicaba que la línea debía ser descartada recorriendo con el dedo las dos primeras columnas y escribía así las doce letras más frecuentes. La mecánica de funcionamiento de las componedoras de Linotype no permitía corregir los errores, por lo que la línea debía ser fundida de todas maneras, y luego descartada antes de armar la matriz de impresión.1 De vez en cuando, una línea defectuosa terminaba siendo impresa, y es así que a lo largo de los años etaoin shrdlu fue apareciendo en diversas publicaciones, como el nombre de alguna criatura lovecraftiana intentando colarse en nuestro mundo.

Origen y proceso de la investigación

El dato anecdótico de etaoin shrdlu me llevó a plantearme una serie de preguntas, y tratar de encontrar sus respuestas: ¿hay cifras disponibles que respalden el criterio de distribución del teclado de las máquinas de linotipo y otras listas de frecuencia de aparición de los caracteres?; ¿estas cifras, que se desprenden del análisis de las palabras existentes en un idioma, son igualmente válidas si se hace el recuento a partir de un texto, en lugar de las entradas de un diccionario?; ¿se mantienen las cifras en diferentes tipos de texto o varían sensiblemente, por ejemplo, entre un texto periodístico y uno técnico o científico?; ¿existen estadísticas similares respecto a pares de caracteres?; ¿cómo podrían aprovechar los diseñadores gráficos estos datos a la hora de elegir qué tipografía usar, y especialmente los diseñadores de tipos al trabajar en un nuevo diseño, o los calígrafos al crear variantes para el dibujo de diversos caracteres?; ¿hay datos equivalentes a partir de textos en español?

Algunas respuestas no fueron demasiado difíciles de encontrar, Google mediante. Más allá de pequeñas diferencias, diversos estudios indican que, en inglés, las primeras doce letras mantienen casi el mismo orden, ya sea que el recuento se base en el Concise Oxford English Dictionary, en una colección de 40.000 palabras como la usada por Treven Wall y Lawren Smithline de la Universidad de Cornell2 o en el colosal corpus de Google Books, de más de 743.000 millones de palabras, usado por Peter Norvig,3 director de investigaciones de Google, en una excelente investigación realizada de diciembre de 2012.4 Para el español, las únicas cifras fácilmente disponibles provienen de un título clave en la literatura sobre criptografía escrito por Fletcher Pratt (1939),5 mejor conocido por sus obras de ciencia ficción, fantasía e historia, e indican, entre otras cosas, que el equivalente hispano de etaoin shrdlu sería eaosrn idltcm.

El resto de las preguntas que rondaban mi cabeza eran más difíciles de responder. Aunque efectivamente hay algunos datos de investigaciones sobre la frecuencia de los caracteres o los fonemas en español, se trata de estudios lingüísticos más que tipográficos. El foco de mi interés era, fundamentalmente, conseguir información útil para el diseño de caracteres tipográficos o caligráficos, tales como los pares de caracteres más habituales, los caracteres más comunes al comienzo o al final de las palabras, a cuyo diseño dedicar más atención, y las combinaciones poco frecuentes, en las que tal vez no se justifique detenerse demasiado. Estos datos deberían ofrecer una ayuda importante a la hora de tomar una decisión informada sobre las prioridades y el tiempo que dedicar a tareas como el diseño de las ligaduras o el ajuste del kerning por pares.

El proceso de diseño de una nueva tipografía suele comenzar con una palabra (Hamburgefonts con sus variantes Hamburgefons y Hamburgefonstiv es, tal vez, la más icónica). ¿No sería bueno que la palabra elegida, además de usar caracteres con todos los elementos básicos del diseño, como la modulación de los trazos, las terminaciones, la altura de equis, la longitud de los ascendentes y descendentes, contuviera también algunos de los pares más frecuentes, para asegurar desde la concepción que los caracteres que en la práctica se usarán lado a lado funcionen fluidamente, como un grupo de piezas que encastran perfectamente?

De la misma manera, al presentar tipografías o evaluarlas durante el proceso de diseño, se suelen usar pangramas (textos breves que incorporan el conjunto completo de caracteres). El texto «El veloz murciélago hindú comía feliz cardillo y kiwi. La cigüeña tocaba el saxofón detrás del palenque de paja» resulta un ejemplo familiar de pangrama para los usuarios de Windows, mientras que «Jovencillo emponzoñado de whisky: ¡qué figurota exhibe!» lo es para los de Linux y Apple. El ejemplo más condensado, en español, probablemente sea «Whisky bueno: ¡excitad mi frágil pequeña vejez!». Pero cuando de evaluar una tipografía en funcionamiento se trata, la brevedad no necesariamente es una ventaja. En cambio, un pangrama que contenga los pares más comunes en un idioma, y que por consiguiente sea más representativo de un texto promedio, resultaría una herramienta más útil a la hora de evaluar el diseño.

Una vieja conversación en Typophile6 me sirvió para confirmar que no era yo el único en plantearse este tipo de preguntas. Uno de los participantes en esa conversación, Michel Boyer, incluso creó una herramienta en línea7 capaz de hacer el recuento de pares de caracteres de cualquier texto en internet, aunque con ciertas limitaciones que le impiden dar respuesta a algunas de mis inquietudes.

Al continuar en la búsqueda de esas respuestas, me resultó casi imposible hallar datos relativos a la frecuencia de pares de caracteres en el español. Lo más cercano a mi interés que pude encontrar fue un trabajo de Francisco Gutiérrez Muñoz, Gloria del Rey Gutiérrez y Alfredo del Rey Guerrero,8 del Instituto de Ciencia y Tecnología de Madrid, publicado en 1989, pero centrado específicamente en el análisis de títulos de artículos científicos y técnicos.

Al mirar el camino recorrido hasta el momento, se hizo evidente que los datos disponibles, por una razón u otra, no eran adecuados para mis propósitos: la excelente investigación de Peter Norvig mencionada más arriba se enfoca específicamente en el inglés; los datos recabados por Google Books, son, por su enormidad, abrumadores para la modestia de mi curiosidad; la información disponible en otras fuentes es limitada. En todos los casos, por tratarse de investigaciones desde una orientación lingüística y no tipográfica, las mayúsculas y minúsculas se consideran como una misma entidad, por lo que se pierde una diferenciación importante para mis objetivos.

El siguiente paso, entonces, era encontrar una herramienta adecuada o desarrollar una nueva. Si bien existen numerosas aplicaciones para el análisis de textos, muchas de ellas de uso gratuito, mis requerimientos eran muy específicos y relativamente modestos en términos de los procesos que realizar y los datos que reunir, y no justificaban el uso y la consiguiente curva de aprendizaje de este tipo de aplicaciones orientadas al manejo y análisis de grandes bancos de datos para el desarrollo del back-end para motores de búsqueda o el análisis lingüístico de contenidos. La solución, entonces, era desarrollar una aplicación sencilla que, a partir de un archivo de texto y un conjunto de caracteres determinado, produjera listados del número de apariciones de cada carácter individual o de cada par de caracteres posible. Tras un primer intento, junto a mi hija Catalina, de desarrollar la aplicación por nuestra cuenta, decidí recurrir a la ayuda de un buen amigo, dedicado profesionalmente a la programación, Leonardo de Vida. Así surgió entonces la aplicación usada para reunir los datos estadísticos de esta investigación.9

Con esta solución, se obtienen listados que pueden compilarse en tablas para obtener totales generales, calcular frecuencias y hacer diversos análisis. Para garantizar flexibilidad, el set de caracteres que utilizar se define en un archivo de texto independiente, lo que permite adaptarlo a las necesidades de cada caso, ya sea por caracteres especiales correspondientes a un idioma en particular o simplemente para analizar un subconjunto de caracteres específicos. Para garantizar un máximo de compatibilidad entre plataformas, la aplicación fue programada en Java, y si bien por defecto utiliza la codificación de texto del sistema, puede forzarse el uso de UTF-8, lo que asegura un máximo de compatibilidad con diversos juegos de caracteres correspondientes a diferentes idiomas y sistemas operativos.

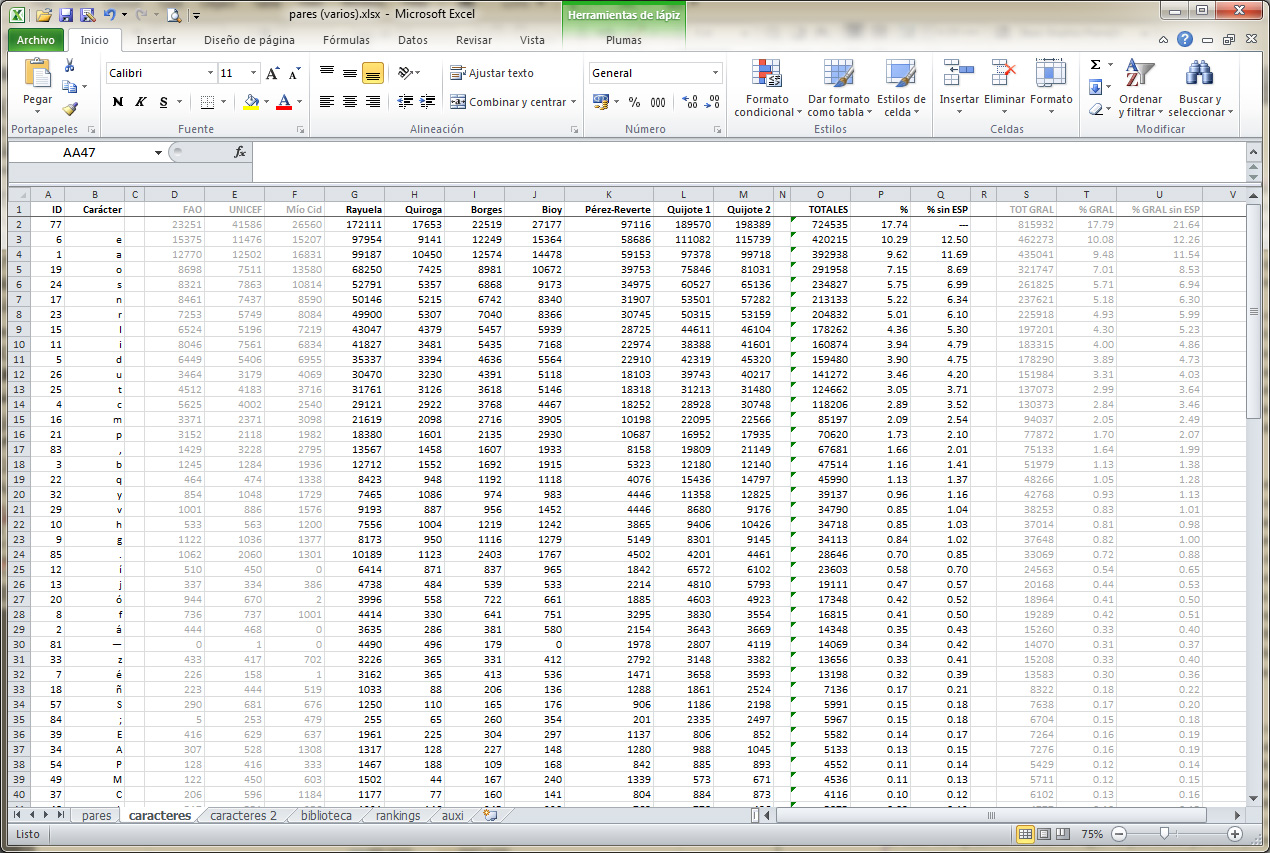
Ya con la aplicación en funcionamiento, el siguiente paso fue compilar una selección reducida pero representativa de textos en los que basar el análisis. El Quijote de Cervantes encabezó la lista, por tratarse de una de las piezas literarias culturalmente más icónicas del español, además de tener una extensión suficiente para proveer datos útiles con una proporción mínima de casos especiales. Completaron la lista otras obras más contemporáneas: Cuentos de la selva de Quiroga, El informe de Brodie de Borges, La invención de Morel de Bioy Casares, Rayuela de Cortázar y Un día de cólera de Pérez-Reverte. Para complementar estos textos, decidí incluir en el análisis, pero dejar de lado en el cálculo inicial de totales, algunos títulos con un alto potencial de producir cifras sensiblemente alejadas del promedio: Perspectivas de cosechas y situación alimentaria de la FAO, El estado mundial de la infancia de 2014 en cifras de UNICEF y el Cantar de Mio Cid; los dos primeros fundamentalmente por tratarse de documentos cargados de cifras y, en menor medida, por una posible repetición de términos específicos y nombres propios, y el último por tratarse de un texto en español del siglo xii.

Una vez procesados los textos elegidos y organizados los datos resultantes, y antes de iniciar cualquier otro análisis, correspondía verificar su validez. La forma más lógica de proceder era comparar los datos obtenidos con datos similares disponibles de otras fuentes. Mis datos eran un recuento de caracteres, en el que se incluían números, signos de puntuación, paréntesis y otros caracteres no alfabéticos, se consideraban independientemente mayúsculas y minúsculas, y en el caso de las vocales las apariciones con y sin tilde figuraban como entidades independientes. Las cifras de Pratt, en cambio, solamente consideran letras (a modo de ejemplo: la palabra acá tiene tres caracteres diferentes: a, c y á, pero solamente dos letras distintas: a y c). Esta diferencia requirió de cierta compilación antes de hacer el cálculo de totales y porcentajes para poder hacer una comparación entre ambos conjuntos de valores. Los resultados, si bien no idénticos, coinciden en promedio en un 99,65%, lo que confirma que los datos son adecuados para proceder a un análisis más detallado y obtener resultados válidos.

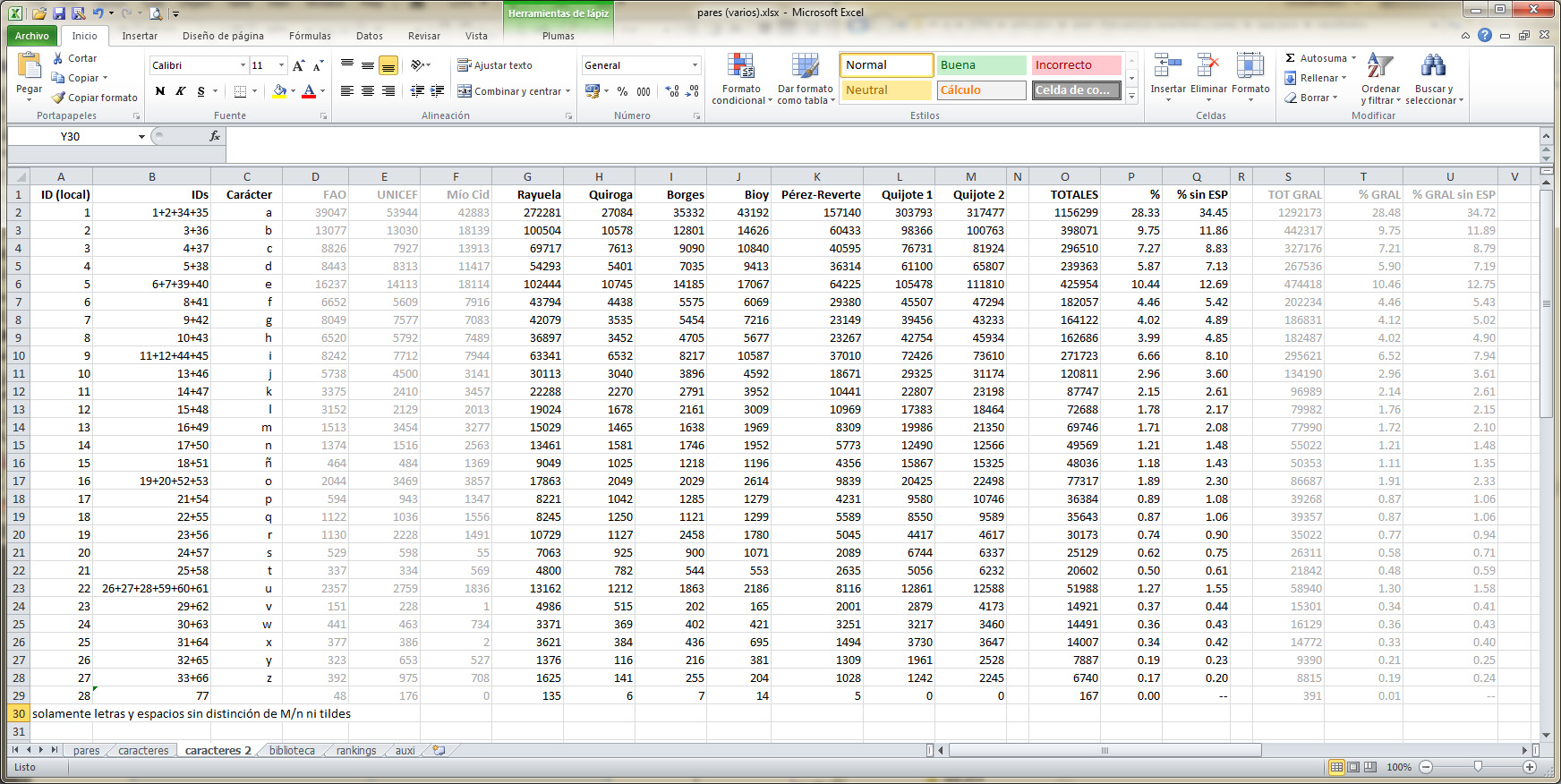
Como mencioné antes, según datos ya existentes, el equivalente hispano de etaoin shrdlu sería eaosrn idltcm. De mi análisis se desprende un orden apenas diferente: eaosnr ildutc mpqbyv hgjfzñ xkw. Vale hacer notar que las cinco letras más frecuentes (e, a, o, s, n) representan un 50% del total de los textos analizados (solamente la e y la a, sumadas, superan el 25%), y que ninguna de las 13 letras en la mitad más baja de la lista alcanza el 2%; más aún, x, k y w ni siquiera alcanzan el 0,1%.

Resultados de la investigación

Al analizar los datos generales, diferenciando mayúsculas y minúsculas, enfocándonos en caracteres en lugar de letras (lo que implica, por ejemplo, considerar las vocales con y sin tilde como entidades diferentes) y teniendo en cuenta un juego más amplio de caracteres que el simple alfabeto,10 y observar los valores correspondientes a pares de caracteres, se pueden constatar algunos datos interesantes:

Mayúsculas y minúsculas

Los caracteres alfabéticos más comunes son, sobra decirlo, las minúsculas, y estas presentan una frecuencia de aparición casi idéntica a la señalada más arriba para los totales sin diferenciar. Las mayúsculas, en cambio, se ordenan por frecuencia de aparición de manera notablemente diferente a las cifras generales: SEAPMCLDQTNYORVBGHFIJUZXWKÑ. Sumadas, las mayúsculas apenas alcanzan el 1,58% del total de caracteres analizados.

A la luz de esto, resulta oportuno resaltar algo de suma importancia que tener en cuenta para cualquier aplicación práctica de los datos conseguidos en esta investigación: la baja frecuencia de aparición de un carácter en particular no necesariamente se corresponde con una baja importancia de este; en el caso de las mayúsculas es evidente que su importancia (y la atención necesaria a la hora de encarar su diseño) no proviene de su frecuencia de uso sino de su función, y lo mismo se aplica, en mayor o menor medida, a los caracteres no alfabéticos. La información sobre frecuencia de aparición, sin embargo, puede resultar muy útil a la hora de estimar la importancia relativa de diferentes caracteres dentro de una misma categoría.

Caracteres no alfabéticos

Los caracteres no alfabéticos más comunes son, de mayor a menor frecuencia: el espacio (17,74%, más de 7 puntos por delante de la letra más frecuente, la e, con 10,29%), la coma (en el puesto 16, con 1,66%), el punto (en la posición 23, 0,7%), la raya (29, 0,34%), el punto y coma (34, 0,15%) y los dos puntos (44, 0,08%), seguidos por los signos de interrogación, exclamación, comillas, paréntesis y guión, todos ellos por delante de los números y demás signos registrados. A modo de referencia, la mayúscula más frecuente, la S, ocupa el puesto 33, detrás de la ñ (minúscula), con el 0,15%.

Final de palabras

La lista de los caracteres alfabéticos más probables al final de una palabra se ordena del siguiente modo: e, a, o, s, n, l, r, y, i, ó, u, d, é, í, á, z, Y, A, t, ú, h. Nótese que los primeros cinco coinciden, incluso en el orden, con los de uso más frecuente en general, pero el resto de la lista varía sensiblemente. Solamente se incluyeron en esta lista los caracteres con una frecuencia del 0,01% o mayor.

Inicio de palabras

La lista de caracteres más frecuentes al inicio de palabras (aplicando el mismo criterio del 0,01%) es mucho más extensa y variada: d, e, l, a, c, s, p, q, m, y, t, h, v, n, u, r, o, f, b, i, g, S, M, E, P, A, D, C, L, Q, T, j, é, Y, R, N, B, G, O, F, V, H, J, U, I, ú, á, z, 1, í. Como era de esperar, hay un mayor número de mayúsculas, gracias a los nombres propios y el comienzo de las oraciones. Es interesante destacar que el conjunto de letras minúsculas dentro de esta lista es notoriamente diferente al de las mayúsculas.

Pares de caracteres

Los 50 pares de caracteres más frecuentes son: de, en, es, ue, er, os, la, qu, ra, an, as, de, ar, el, on, nt, re, co, ta, or, te, se, al, lo, st, ad, ro, to, le, ie, no, ca, da, nd, un, ab, ci, me, na, po, in, di, tr, pa, sa, ha, ma, mo, ll, si. La frecuencia de aparición va desde el 1,63% para el par de hasta el 0,37% para si.

Como hecho curioso, la única ligadura tradicional dentro de esta lista de pares más frecuentes es st, y ninguno de los pares de la lista ni siquiera incluye la f, motivo de la mayoría de las ligaduras clásicas. No obstante, la lista sí debería ser útil para establecer prioridades en el proceso de ajuste del kerning por pares.

Pares mayúscula-minúscula

Hay 69 pares compuestos por una mayúscula y una minúscula que figuran con una frecuencia del 0,01% o mayor: Qu, Sa, Ma, Es, No, Pe, En, El, La, Ca, Pa, De, Lo, Di, Ol, Po, Co, Ro, Mo, Tr, Al, Se, To, Si, Ta, An, Ha, Mi, Re, Me, Do, Yo, Un, Cu, Ba, Lu, Le, Te, Fe, Gr, Du, Vi, Ar, Ve, Pu, So, Be, Ho, Ju, Ah, Su, Pr, As, Da, Ga, Vo, Ya, Ce, Gu, Fr, Mu, Va, Bu, Jo, Fa, He, Cl, Et, Ll.

Sin lugar a duda, estos son solamente algunos de los datos que se pueden obtener a partir del análisis de las cifras recogidas. El procesamiento de un mayor número de títulos podría resultar en datos más precisos, y la inclusión de cifras correspondientes a otros idiomas en un mayor espectro de aplicación. El trabajo, entonces, recién comienza.

Notas

1. Para quien tenga curiosidad por saber más sobre estos equipos y su funcionamiento, existe un excelente documental de la época, disponible en línea: https://archive.org/details/Typesett1960 y https://archive.org/details/Typesett1960_2
2. http://www.math.cornell.edu/~mec/2003-2004/cryptography/polyalpha/polyalpha.html
3. http://norvig.com/mayzner.html
4. Esta investigación fue inspirada por una carta de Mark Mayzner, un investigador actualmente retirado, autor de varias investigaciones, en los años 1960, sobre la frecuencia de las letras y los pares de letras en inglés, y autor del artículo Tables of Single-letter and Digram Frequency Counts for Various Word-length and Letter-position Combinations, publicado en 1965 en Psychonomic Monograph Supplements 1(2), pp. 3-32.
5. Pratt, F. (1939). Secret and Urgent: the Story of Codes and Ciphers, pp. 254-255. Indianápolis, Nueva York: Blue Ribbon Books.
6. http://www.typophile.com/node/61027
7. http://www.iro.umontreal.ca/~boyer/typophile/bigrams/
8. http://digital.csic.es/bitstream/10261/23931/1/SAD_DIG_IEDCyT_Gutierrez_Revista%20Espa%C3%B1ola%20de%20Documentacion%20Cientifica12%282%29.pdf
9. Esa aplicación está disponible en forma gratuita para quien tenga interés en reunir sus propios datos.
10. Para el análisis de los textos elegidos utilicé el siguiente juego de caracteres: aábcdeéfghiíjklmnñoópqrstuúüvwxyzAÁBCDEÉFGHIÍJKLMNÑOÓPQRSTUÚÜVWXYZ0123456789 +-–—/,;.:¡!¿?\«»“”$%&*(){}[]_